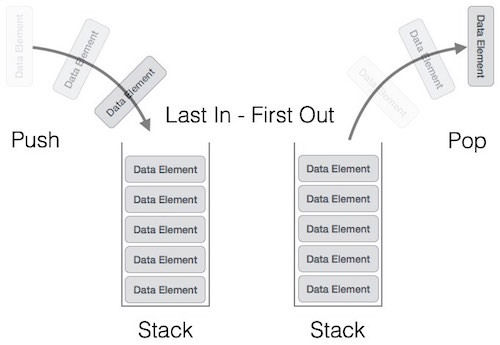
Stack is a linear data structure which follows a particular order in which the operations are performed. The order may be LIFO(Last In First Out) or FILO(First In Last Out).
前言 栈(stack)在计算机科学中是限定仅在表尾进行插入或删除操作的线性表。栈是一种数据结构,它按照后进先出的原则存储数据,先进入的数据被压入栈底,最后的数据在栈顶,需要读数据的时候从栈顶开始弹出数据。栈是只能在某一端插入和删除的特殊线性表。
栈 栈的应用场景:
1)子程序的调用:在跳往子程序前,会先将下个指令的地址存到堆栈中,直到子程序执行完后再将地址取出,以回到原来的程序中;
2)处理递归调用:和子程序的调用类似,只是除了储存下一个指令的地址外,也将参数、区域变量等数据存入堆栈中;
3)表达式的转换[中缀表达式转后缀表达式]与求值(实际解决);
4)二叉树的遍历;
5)图形的深度优先一搜索法。
栈图解:
实现 栈的 思路分析:
使用数组来模拟栈;
定义一个 top 来表示栈顶,初始化 为 -1;
入栈的操作,当有数据加入到栈时, top++; stack[top] = data;
出栈的操作, int value = stack[top]; top–, return value。
数组,链表模拟栈代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 import java.util.Scanner;import java.util.Stack;public class StackDemo public static void main (String[] args) LinkedListStack arrayStack = new LinkedListStack(); boolean loop = true ; String key; Scanner scanner = new Scanner(System.in); while (loop) { System.out.println("输入push为入栈" ); System.out.println("输入pop为出栈" ); System.out.println("输入list为查看" ); System.out.println("输入exit为退出" ); key = scanner.next(); switch (key) { case "push" : int value = scanner.nextInt(); arrayStack.push(value); break ; case "pop" : try { arrayStack.pop(); } catch (Exception e) { e.printStackTrace(); } break ; case "list" : arrayStack.list(); break ; default : loop = false ; break ; } } System.out.println("程序运行结束" ); } } class ArrayStack private int top = -1 ; private int size; private int [] stack; public ArrayStack (int size) if (size < 1 ) { System.out.println("数据有误" ); return ; } this .size = size; stack = new int [this .size]; } public boolean isFull () return top == size - 1 ; } public boolean isEmpty () return top == -1 ; } public void push (int value) if (isFull()) { System.out.println("栈已满" ); return ; } stack[++top] = value; } public int pop () if (isEmpty()) { System.out.println("栈已空" ); throw new RuntimeException("栈已空" ); } return stack[top--]; } public void list () if (isEmpty()) { System.out.println("栈已空" ); return ; } for (int i = top; i >= 0 ; i--) { System.out.printf("stack[%d]=%d\n" , i, stack[i]); } } } class LinkedListStack Node head = new Node(-1 ); public boolean isEmpty () return head.next == null ; } public void push (int no) Node cur = head; while (true ) { if (cur.next == null ) { break ; } cur = cur.next; } Node node = new Node(no); cur.next = node; } public Node pop () if (isEmpty()) { System.out.println("栈已空" ); throw new RuntimeException("栈已空" ); } Node cur = head; while (true ) { if (cur.next.next == null ) { break ; } cur = cur.next; } Node temp = cur.next; cur.next = null ; return temp; } public void list () if (isEmpty()) { System.out.println("栈已空" ); return ; } Stack<Integer> stack = new Stack<>(); Node cur = head; int i = -1 ; while (true ) { stack.push(cur.no); if (cur.next == null ) { break ; } i++; cur = cur.next; } for (int j = i; j >= 0 ; j--) { System.out.println("stack[" + j + "]=" + stack.pop()); } } } class Node public int no; public Node next; public Node (int no) this .no = no; } }
栈实现综合计算器 思路:
通过一个 index 值(索引),来遍历我们的表达式;
如果我们发现是一个数字, 就直接入数栈;
如果发现扫描到是一个符号, 就分如下情况;
1 如果发现当前的符号栈为 空,就直接入栈;
2 如果符号栈有操作符,就进行比较,如果当前的操作符的优先级小于或者等于栈中的操作符, 就需要从数栈中pop出两个数,在从符号栈中pop出一个符号,进行运算,将得到结果,入数栈,然后将当前的操作符入符号栈, 如果当前的操作符的优先级大于栈中的操作符, 就直接入符号栈;
当表达式扫描完毕,就顺序的从 数栈和符号栈中pop出相应的数和符号,并运行;
最后在数栈只有一个数字,就是表达式的结果。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 public class Calculator public static void main (String[] args) String expression = "7*2*2-5+1-5+3-4" ; ArrayCalculatorStack numberStack = new ArrayCalculatorStack(10 ); ArrayCalculatorStack operatorStack = new ArrayCalculatorStack(10 ); int index = 0 ; int num1 = 0 ; int num2 = 0 ; int oper = 0 ; int res = 0 ; char ch = ' ' ; String keepNum = "" ; while (true ) { ch = expression.substring(index, index + 1 ).charAt(0 ); if (operatorStack.isOperator(ch)) { if (!operatorStack.isEmpty()) { if (operatorStack.priority(ch) <= operatorStack.priority(operatorStack.peek())) { num1 = numberStack.pop(); num2 = numberStack.pop(); oper = operatorStack.pop(); res = operatorStack.calculate(num1, num2, oper); numberStack.push(res); operatorStack.push(ch); } else { operatorStack.push(ch); } } else { operatorStack.push(ch); } } else { keepNum += ch; if (index == expression.length() - 1 ) { numberStack.push(Integer.parseInt(keepNum)); } else { if (operatorStack.isOperator(expression.substring(index + 1 , index + 2 ).charAt(0 ))) { numberStack.push(Integer.parseInt(keepNum)); keepNum = "" ; } } } index++; if (index >= expression.length()) { break ; } } while (true ) { if (operatorStack.isEmpty()) { break ; } num1 = numberStack.pop(); num2 = numberStack.pop(); oper = operatorStack.pop(); res = numberStack.calculate(num1, num2, oper); numberStack.push(res); } int res2 = numberStack.pop(); System.out.printf("表达式 %s = %d" , expression, res2); } } class ArrayCalculatorStack private int maxSize; private int [] stack; private int top = -1 ; public ArrayCalculatorStack (int maxSize) if (maxSize <= 0 ) { System.out.println("栈的大小设置有误!" ); return ; } this .maxSize = maxSize; stack = new int [maxSize]; } public boolean isFull () return top == maxSize - 1 ; } public boolean isEmpty () return top == -1 ; } public void push (int value) if (isFull()) { System.out.println("栈已满" ); return ; } stack[++top] = value; } public int pop () if (isEmpty()) { System.out.println("栈已空" ); throw new RuntimeException("栈已空" ); } return stack[top--]; } public void list () if (isEmpty()) { System.out.println("栈已空" ); return ; } for (int i = top; i >= 0 ; i--) { System.out.printf("stack[%d]=%d\n" , i, stack[i]); } } public int peek () if (isEmpty()) { System.out.println("栈已空" ); throw new RuntimeException("栈已空" ); } return stack[top]; } public int priority (int oper) if (oper == '*' || oper == '/' ) { return 1 ; } else if (oper == '+' || oper == '-' ) { return 0 ; } else { return -1 ; } } public boolean isOperator (char val) return val == '+' || val == '-' || val == '*' || val == '/' ; } public int calculate (int num1, int num2, int operator) int res = 0 ; switch (operator) { case '+' : res = num1 + num2; break ; case '-' : res = num2 - num1; break ; case '*' : res = num1 * num2; break ; case '/' : res = num2 / num1; break ; default : break ; } return res; } }
前缀、中缀、后缀表达式 前缀表达式(波兰表达式) 1)前缀表达式又称波兰式,前缀表达式的运算符位于操作数之前;
前缀表达式的计算机求值:
从右至左扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(栈顶元素 和 次顶元素),并将结果入栈;重复上述过程直到表达式最左端,最后运算得出的值即为表达式的结果。
例如: (3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6 , 针对前缀表达式求值步骤如下:
1)从右至左扫描,将6、5、4、3压入堆栈;
中缀表达式 1)中缀表达式就是常见的运算表达式,如(3+4)×5-6;
后缀表达式(逆波兰表达式) 1)后缀表达式又称逆波兰表达式,与前缀表达式相似,只是运算符位于操作数之后;
大家看到,后缀表达式适合计算式进行运算,但是人却不太容易写出来,尤其是表达式很长的情况下,因此在开发中,我们需要将 中缀表达式转成后缀表达式。
具体步骤如下:
5)遇到括号时:
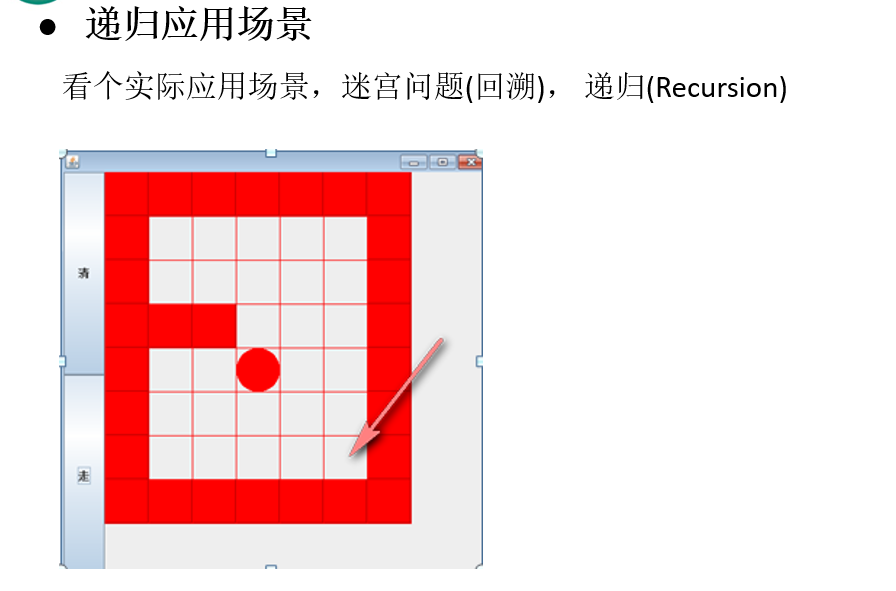
递归-迷宫问题 递归的概念:
递归应用场景:
1)各种数学问题如: 8皇后问题 , 汉诺塔, 阶乘问题, 迷宫问题, 球和篮子的问题(google编程大赛);
递归需要遵守的重要规则
1)执行一个方法时,就创建一个新的受保护的独立空间(栈空间);
迷宫问题:
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 public class Maze public static void main (String[] args) int [][] map = new int [8 ][7 ]; for (int i = 0 ; i < map.length; i++) { map[i][0 ] = 1 ; map[i][6 ] = 1 ; } for (int i = 0 ; i < map[1 ].length; i++) { map[0 ][i] = 1 ; map[7 ][i] = 1 ; } map[3 ][1 ] = 1 ; map[3 ][2 ] = 1 ; System.out.println("====初始化地图====" ); showMap(map); setWay(1 , 1 , map); System.out.println("====迷宫出口路线====" ); showMap(map); } public static boolean setWay (int i, int j, int [][] map) if (map[6 ][5 ] == 2 ) { return true ; } else { if (map[i][j] == 0 ) { map[i][j] = 2 ; if (setWay(i + 1 , j, map)) { return true ; } else if (setWay(i, j + 1 , map)) { return true ; } else if (setWay(i - 1 , j, map)) { return true ; } else if (setWay(i, j - 1 , map)) { return true ; } else { map[i][j] = 3 ; return false ; } } else { return false ; } } } public static void showMap (int [][] map) if (map == null ) { System.out.println("地图未初始化" ); return ; } for (int i = 0 ; i < map.length; i++) { for (int j = 0 ; j < map[i].length; j++) { System.out.print(map[i][j] + " " ); } System.out.println(); } } }
迷宫最短路径问题 四种策略下,路径最短问题:
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 import java.util.HashMap;import java.util.Map;public class OptimalPathMaze public static void main (String[] args) Map<String, Object> result = new HashMap<>(); int [][] map = initialMap(); System.out.println("初始化地图" ); showMap(map); System.out.println("策略是->下右上左" ); setWay1(1 , 1 , map); showMap(map); int pathStep = getPathStep(map); result.put("策略:下右上左; 步数为:" , pathStep); System.out.println("策略是->上右下左" ); map = initialMap(); setWay2(1 , 1 , map); showMap(map); pathStep = getPathStep(map); result.put("策略:上右下左; 步数为:" , pathStep); System.out.println("策略是->右下左上" ); map = initialMap(); setWay3(1 , 1 , map); showMap(map); pathStep = getPathStep(map); result.put("策略:右下左上; 步数为:" , pathStep); System.out.println("策略是->左上右下" ); map = initialMap(); setWay4(1 , 1 , map); showMap(map); pathStep = getPathStep(map); result.put("策略:左上右下; 步数为:" , pathStep); System.out.println(result); } public static boolean setWay4 (int i, int j, int [][] map) if (map[6 ][5 ] == 2 ) { return true ; } else { if (map[i][j] == 0 ) { map[i][j] = 2 ; if (setWay4(i, j - 1 , map)) { return true ; } else if (setWay4(i + 1 , j, map)) { return true ; } else if (setWay4(i, j + 1 , map)) { return true ; } else if (setWay4(i + 1 , j, map)) { return true ; } else { map[i][j] = 3 ; return false ; } } else { return false ; } } } public static boolean setWay3 (int i, int j, int [][] map) if (map[6 ][5 ] == 2 ) { return true ; } else { if (map[i][j] == 0 ) { map[i][j] = 2 ; if (setWay3(i, j + 1 , map)) { return true ; } else if (setWay3(i + 1 , j, map)) { return true ; } else if (setWay3(i, j - 1 , map)) { return true ; } else if (setWay3(i - 1 , j, map)) { return true ; } else { map[i][j] = 3 ; return false ; } } else { return false ; } } } public static boolean setWay2 (int i, int j, int [][] map) if (map[6 ][5 ] == 2 ) { return true ; } else { if (map[i][j] == 0 ) { map[i][j] = 2 ; if (setWay2(i - 1 , j, map)) { return true ; } else if (setWay2(i, j + 1 , map)) { return true ; } else if (setWay2(i + 1 , j, map)) { return true ; } else if (setWay2(i, j - 1 , map)) { return true ; } else { map[i][j] = 3 ; return false ; } } else { return false ; } } } public static boolean setWay1 (int i, int j, int [][] map) if (map[6 ][5 ] == 2 ) { return true ; } else { if (map[i][j] == 0 ) { map[i][j] = 2 ; if (setWay1(i + 1 , j, map)) { return true ; } else if (setWay1(i, j + 1 , map)) { return true ; } else if (setWay1(i - 1 , j, map)) { return true ; } else if (setWay1(i, j - 1 , map)) { return true ; } else { map[i][j] = 3 ; return false ; } } else { return false ; } } } public static int [][] initialMap() { int [][] map = new int [8 ][7 ]; for (int i = 0 ; i < map.length; i++) { map[i][0 ] = 1 ; map[i][6 ] = 1 ; } for (int i = 0 ; i < map[1 ].length; i++) { map[0 ][i] = 1 ; map[7 ][i] = 1 ; } map[3 ][1 ] = 1 ; map[3 ][2 ] = 1 ; return map; } public static void showMap (int [][] map) if (map == null ) { System.out.println("地图未初始化" ); return ; } for (int i = 0 ; i < map.length; i++) { for (int j = 0 ; j < map[i].length; j++) { System.out.print(map[i][j] + " " ); } System.out.println(); } } public static int getPathStep (int [][] map) int step = 0 ; for (int i = 0 ; i < map.length; i++) { for (int j = 0 ; j < map[i].length; j++) { if (map[i][j] == 2 ) { step++; } } } return step; } }
递归-八皇后问题(回溯算法) 八皇后问题算法思路分析:
1)第一个皇后先放第一行第一列;
说明:理论上应该创建一个二维数组来表示棋盘,但是实际上可以通过算法,用一个一维数组即可解决问题. arr[8] = {0 , 4, 7, 5, 2, 6, 1, 3} //对应arr 下标 表示第几行,即第几个皇后,arr[i] = val , val 表示第i+1个皇后,放在第i+1行的第val+1列。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 public class Queue8 int max = 8 ; int [] array = new int [max]; static int count = 0 ; static int judgeCount = 0 ; public static void main (String[] args) Queue8 queue8 = new Queue8(); queue8.check(0 ); System.out.printf("一共有%d解法" , count); System.out.printf("一共判断冲突的次数%d次" , judgeCount); } private void check (int n) if (n == max) { print(); return ; } for (int i = 0 ; i < max; i++) { array[n] = i; if (judge(n)) { check(n+1 ); } } } private boolean judge (int n) judgeCount++; for (int i = 0 ; i < n; i++) { if (array[i] == array[n] || Math.abs(n-i) == Math.abs(array[n] - array[i]) ) { return false ; } } return true ; } private void print () count++; for (int i = 0 ; i < array.length; i++) { System.out.print(array[i] + " " ); } System.out.println(); } }
延伸 栈的作用 数据结构— 栈 韩顺平数据结构和算法 Data Structure and Algorithms - Stack