Merge Sort is a kind of Divide and Conquer algorithm in computer programrming. It is one of the most popular sorting algorithms and a great way to develop confidence in building recursive algorithms.
前言 归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。归并排序是一种稳定的排序方法。
归并排序 归并排序思想:
1)将待排序的线性表不断地切分成若干个子表,直到每个子表只包含一个元素,这时,可以认为只包含一个元素的子表是有序表。
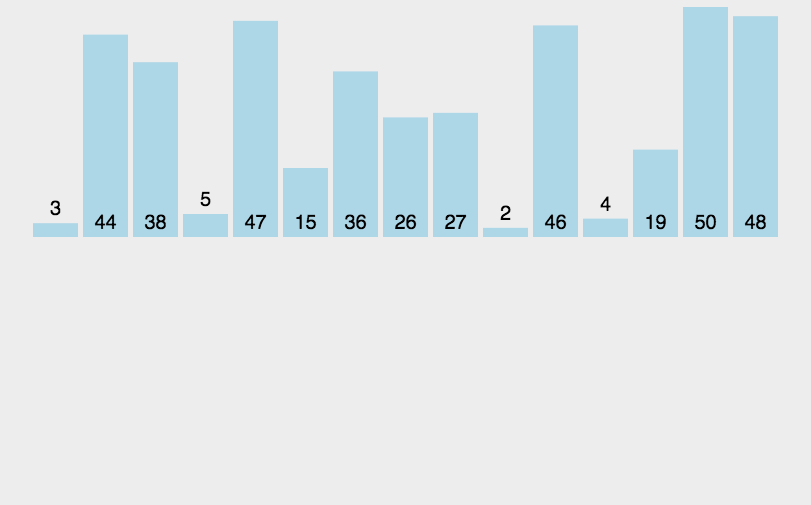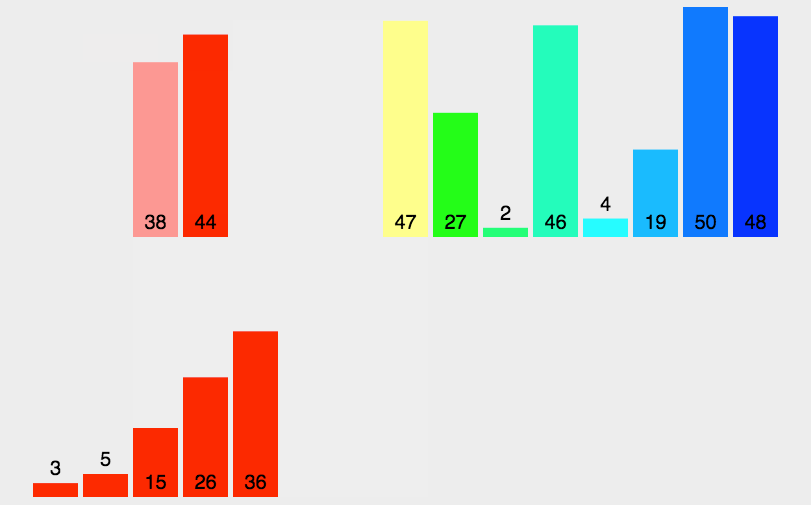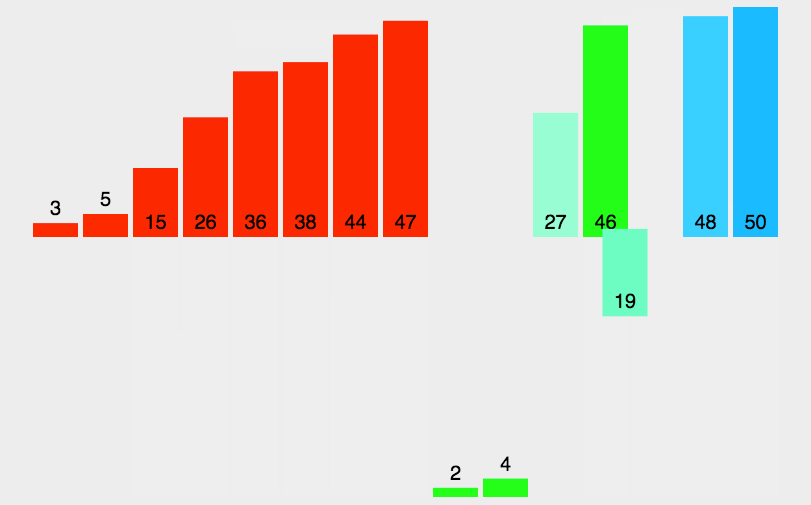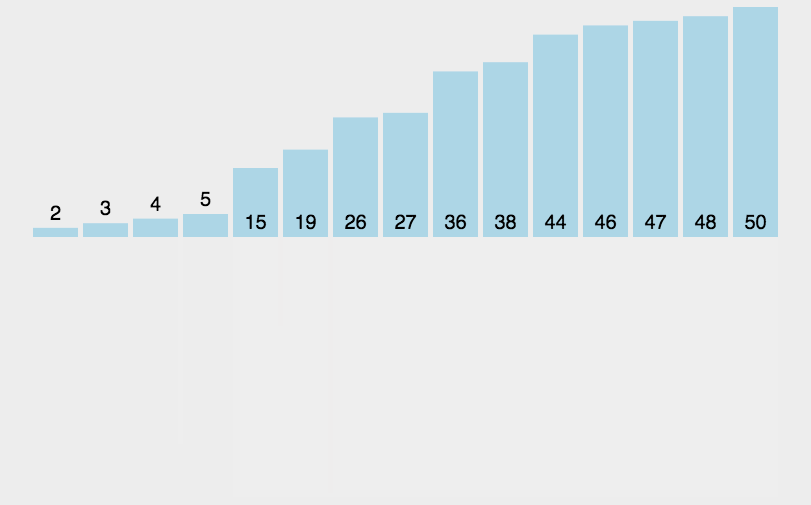
归并排序解析:
归并排序动图:
归并排序代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 public class MergeSort public static void main (String[] args) int [] arr = new int [8000000 ]; for (int i = 0 ; i < 8000000 ; i++) { arr[i] = (int ) (Math.random() * 8000000 ); } long start = System.currentTimeMillis(); int temp[] = new int [arr.length]; mergeSort(arr, 0 , arr.length - 1 , temp); long end = System.currentTimeMillis(); System.out.println("8000000个数字排序所用时间:" + (end - start)); } public static void mergeSort (int [] arr, int left, int right, int [] temp) if (left < right) { int mid = (left + right) / 2 ; mergeSort(arr, left, mid, temp); mergeSort(arr, mid + 1 , right, temp); merge(arr, left, mid, right, temp); } } public static void merge (int [] arr, int left, int mid, int right, int [] temp) int i = left; int j = mid + 1 ; int t = 0 ; while (i <= mid && j <= right) { if (arr[i] <= arr[j]) { temp[t] = arr[i]; t += 1 ; i += 1 ; } else { temp[t] = arr[j]; t += 1 ; j += 1 ; } } while (i <= mid) { temp[t] = arr[i]; t += 1 ; i += 1 ; } while (j <= right) { temp[t] = arr[j]; t += 1 ; j += 1 ; } t = 0 ; int tempLeft = left; while (tempLeft <= right) { arr[tempLeft] = temp[t]; t += 1 ; tempLeft += 1 ; } } }
延伸 Merge Sort 图解 归并排序 Merge Sort Algorithm 韩顺平数据结构和算法 Data Structures - Merge Sort Algorithm
<
Algorithm Radix Sort
Algorithm Quick Sort
>