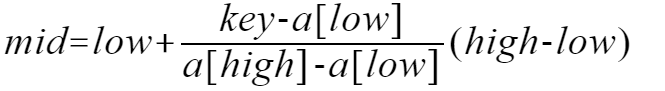Algorithm Interpolation Search
Interpolation search is an improved variant of binary search. This search algorithm works on the probing position of the required value. For this algorithm to work properly, the data collection should be in a sorted form and equally distributed.
前言 插值搜索,有序表的一种查找方式。插值查找是根据查找关键字与查找表中最大最小记录关键字比较后的查找方法。插值查找基于二分查找,将查找点的选择改进为自适应选择,提高查找效率。
插值搜索 插值搜索基本思想:
对于插值查找,就是对于二分查找的优化,将二分查找中的mid = (low + high) / 2改为mid = low + (high - low) * (key - a[low]) / (a[high] - a[low])。插值查找是根据查找关键子key与查找表中最大最小记录关键字比较后的查找方法,核心在于插值计算公式(key-a[low])/(a[high] - a[low])。时间复杂度依旧为O(logn)。 对于表长较大,而关键字分部比较均匀的查找表来说,平均性能要比折半好很多。如果数组中的分部类似{1,100,200,1000,10000…10000}这种极端不均匀的数据,用插值法也不太合适。
插值搜索解析:
插值搜索代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 public class InterpolationSearch public static void main (String[] args) int [] arr = new int [100 ]; for (int i = 0 ; i < 100 ; i++) { arr[i] = i; } int resIndex = interpolationSearch(arr, 0 , arr.length - 1 , 50 ); System.out.println("resIndex:" + resIndex); } public static int interpolationSearch (int [] arr, int low, int high, int key) while (low <= high) { int mid = low + (key - arr[low]) / (arr[high] - arr[low]) * (high - low); if (arr[mid] > key) { high = mid - 1 ; } else if (arr[mid] < key) { low = mid + 1 ; } else { return mid; } } return -1 ; } public static int recusionInterpolationSearch (int [] arr, int low, int high, int key) System.out.println("hello" ); if (low > high || key < arr[0 ] || key > arr[arr.length - 1 ]) { return -1 ; } int mid = low + (key - arr[low]) / (arr[high] - arr[low]) * (high - low); if (arr[mid] > key) { return recusionInterpolationSearch(arr, low, mid - 1 , key); } else if (arr[mid] < key) { return recusionInterpolationSearch(arr, mid + 1 , high, key); } else { return mid; } } }
延伸 插值查找 插值查找 算法-查找-插值查找 韩顺平数据结构和算法 Data Structure - Interpolation Search
<
Algorithm Fibonacci Search
Algorithm Binary Search
>