Dynamic programming approach is similar to divide and conquer in breaking down the problem into smaller and yet smaller possible sub-problems. But unlike, divide and conquer, these sub-problems are not solved independently. Rather, results of these smaller sub-problems are remembered and used for similar or overlapping sub-problems.
前言
动态规划,将大问题划分为小问题进行解决,从而一步步获取最优解的处理算法。
动态规划算法
动态规划算法介绍
1)动态规划(Dynamic Programming)算法的核心思想是:将大问题划分为小问题进行解决,从而一步步获取最优解的处理算法;
2)动态规划算法与分治算法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解;
3)与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。 ( 即下一个子阶段的求解是建立在上一个子阶段的解的基础上,进行进一步的求解 );
4)动态规划可以通过填表的方式来逐步推进,得到最优解。
动态规划算法背包问题:
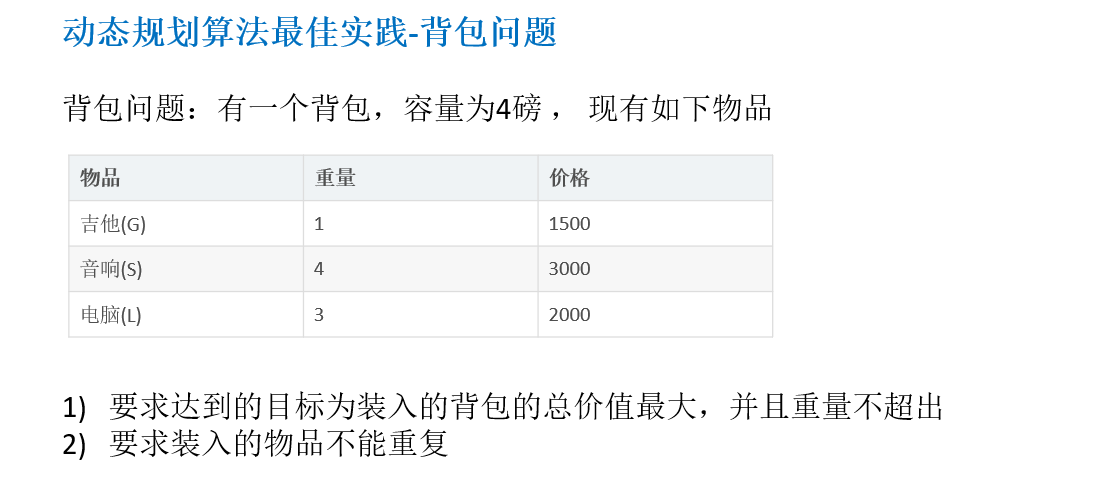
思路分析
算法的主要思想,利用动态规划来解决。每次遍历到的第i个物品,根据w[i]和v[i]来确定是否需要将该物品放入背包中。即对于给定的n个物品,设v[i]、w[i]分别为第i个物品的价值和重量,C为背包的容量。再令v[i][j]表示在前i个物品中能够装入容量为j的背包中的最大价值。则我们有下面的结果:
(1) v[i][0]=v[0][j]=0; //表示 填入表 第一行和第一列是0;
(2) 当w[i]> j 时:v[i][j]=v[i-1][j] // 当准备加入新增的商品的容量大于 当前背包的容量时,就直接使用上一个单元格的装入策略;
(3) 当j>=w[i]时: v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]} 。// 当 准备加入的新增的商品的容量小于等于当前背包的容量,装入的方式: v[i-1][j]: 就是上一个单元格的装入的最大值;v[i] : 表示当前商品的价值;v[i-1][j-w[i]] : 装入i-1商品,到剩余空间j-w[i]的最大值;当j>=w[i]时: v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]} 。
背包问题代码:
1 | /** |
延伸
图解动态规划
动态规划套路详解
动态规划-百度百科
韩顺平数据结构和算法
Data Structures - Dynamic Programming