Prim’s (also known as Jarník’s) algorithm is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. The algorithm operates by building this tree one vertex at a time, from an arbitrary starting vertex, at each step adding the cheapest possible connection from the tree to another vertex.
前言
普里姆算法(Prim算法),图论中的一种算法,可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点(英语:Vertex (graph theory)),且其所有边的权值之和亦为最小。
普里姆算法
普里姆算法介绍
1)普利姆(Prim)算法求最小生成树,也就是在包含n个顶点的连通图中,找出只有(n-1)条边包含所有n个顶点的连通子图,也就是所谓的极小连通子图
2)普利姆的算法如下:
(1)设G=(V,E)是连通网,T=(U,D)是最小生成树,V,U是顶点集合,E,D是边的集合 ;
(2)若从顶点u开始构造最小生成树,则从集合V中取出顶点u放入集合U中,标记顶点v的visited[u]=1;
(3)若集合U中顶点ui与集合V-U中的顶点vj之间存在边,则寻找这些边中权值最小的边,但不能构成回路,将顶点vj加入集合U中,将边(ui,vj)加入集合D中,标记visited[vj]=1;
(4)重复步骤(2),直到U与V相等,即所有顶点都被标记为访问过,此时D中有n-1条边。
普里姆算法图解:
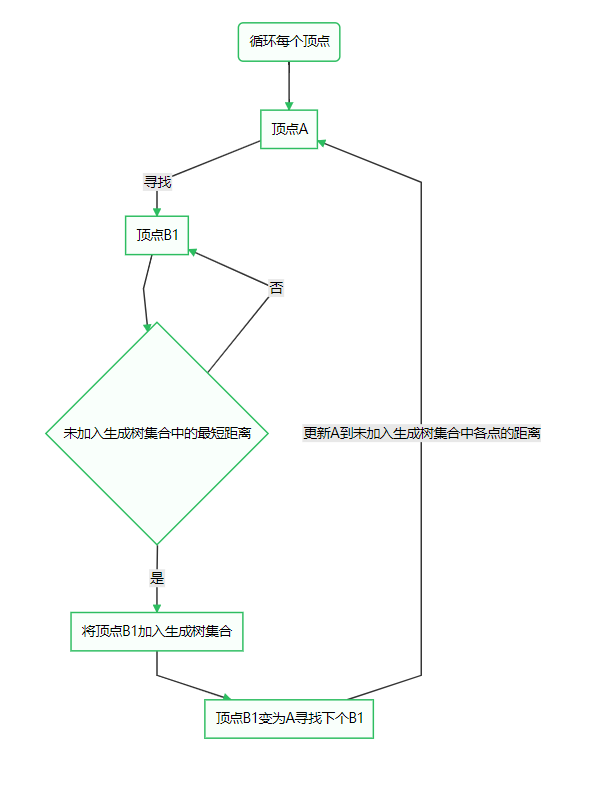
修路问题:
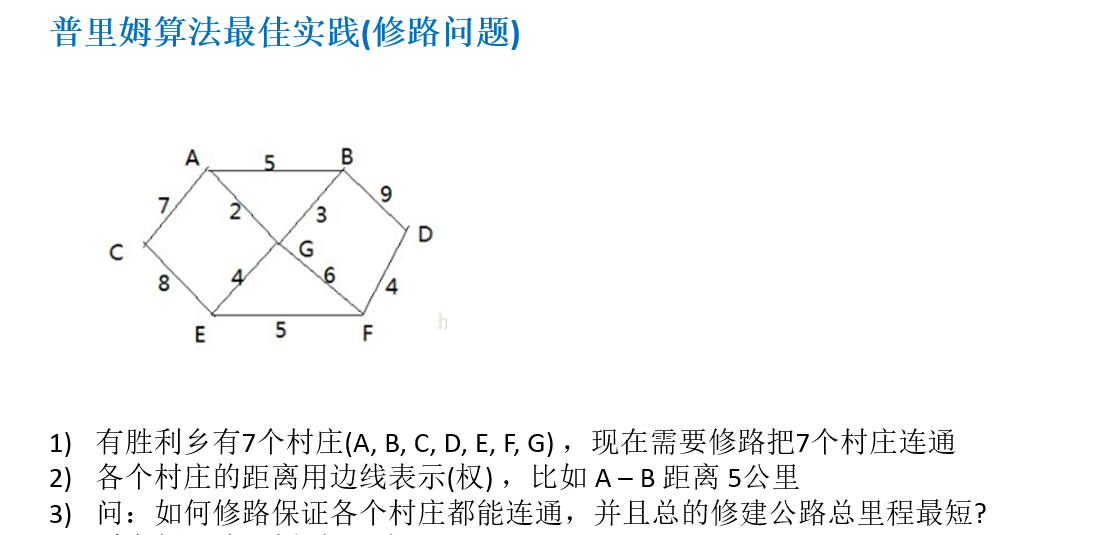
普里姆算法代码:
1 | import java.util.Arrays; |
延伸
Prim算法详解
普里姆算法-百度百科
韩顺平数据结构和算法
最小生成树(普里姆算法)
Prim’s Spanning Tree Algorithm