Floyd’s algorithm is an algorithm for finding shortest paths in a weighted graph with positive or negative edge weights (but with no negative cycles). A single execution of the algorithm will find the lengths (summed weights) of shortest paths between all pairs of vertices.
前言
弗洛伊德算法是一种在具有正或负边缘权重(但没有负周期)的加权图中找到最短路径的算法。算法的单个执行将找到所有顶点对之间的最短路径的长度(加权)。 虽然它不返回路径本身的细节,但是可以通过对算法的简单修改来重建路径。 该算法的版本也可用于查找关系R的传递闭包,或(与Schulze投票系统相关)在加权图中所有顶点对之间的最宽路径。
弗洛伊德算法
弗洛伊德算法介绍:
1)和Dijkstra算法一样,弗洛伊德(Floyd)算法也是一种用于寻找给定的加权图中顶点间最短路径的算法。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名;
2)弗洛伊德算法(Floyd)计算图中各个顶点之间的最短路径;
3)迪杰斯特拉算法用于计算图中某一个顶点到其他顶点的最短路径;
4)弗洛伊德算法 VS 迪杰斯特拉算法:迪杰斯特拉算法通过选定的被访问顶点,求出从出发访问顶点到其他顶点的最短路径;弗洛伊德算法中每一个顶点都是出发访问点,所以需要将每一个顶点看做被访问顶点,求出从每一个顶点到其他顶点的最短路径。
弗洛伊德算法步骤:
1)设置顶点vi到顶点vk的最短路径已知为Lik,顶点vk到vj的最短路径已知为Lkj,顶点vi到vj的路径为Lij,则vi到vj的最短路径为:min((Lik+Lkj),Lij),vk的取值为图中所有顶点,则可获得vi到vj的最短路径;
2)至于vi到vk的最短路径Lik或者vk到vj的最短路径Lkj,是以同样的方式获得;
3)弗洛伊德(Floyd)算法图解分析-举例说明。
弗洛伊德最短路径问题:
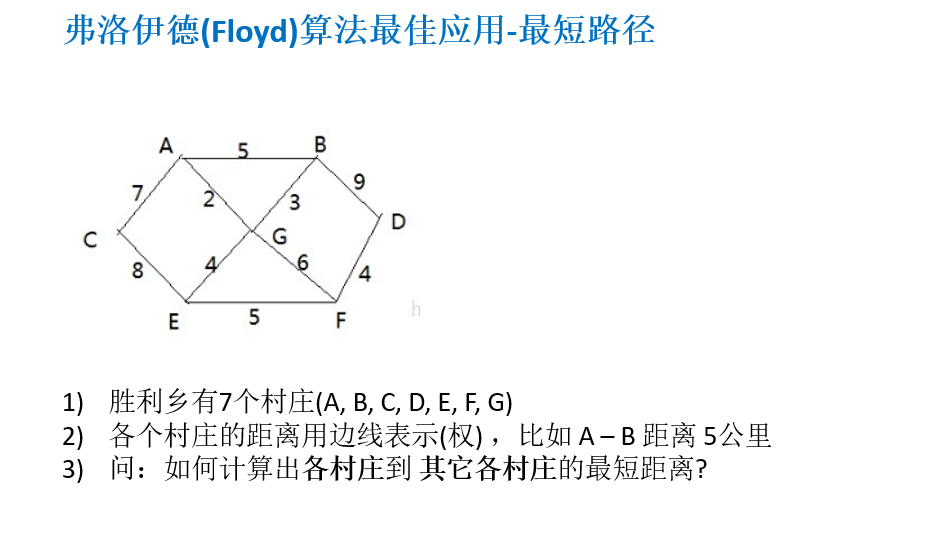
弗洛伊德算法代码:
1 | import java.util.Arrays; |
延伸
弗洛伊德(floyd)算法
Floyd算法-百度百科
韩顺平数据结构和算法
Floyd–Warshall algorithm - Wikipedia
Floyd算法详解——包括解题步骤与编程